
Z 1-p/2 is the standard normal variate corresponding to one minus the proportion of the population to be covered divided by two. However, in practice, a reasonable approximation of k 2 can be obtained using a formula originally proposed by Howe (1969) and later corrected by Guenther (1977): But this calculation, being very complex, is beyond the scope of this article. These values of k 2 were calculated iteratively using a numerical integration process described by Garaj and Janiga in 2002.
Tolerance interval plot iso#
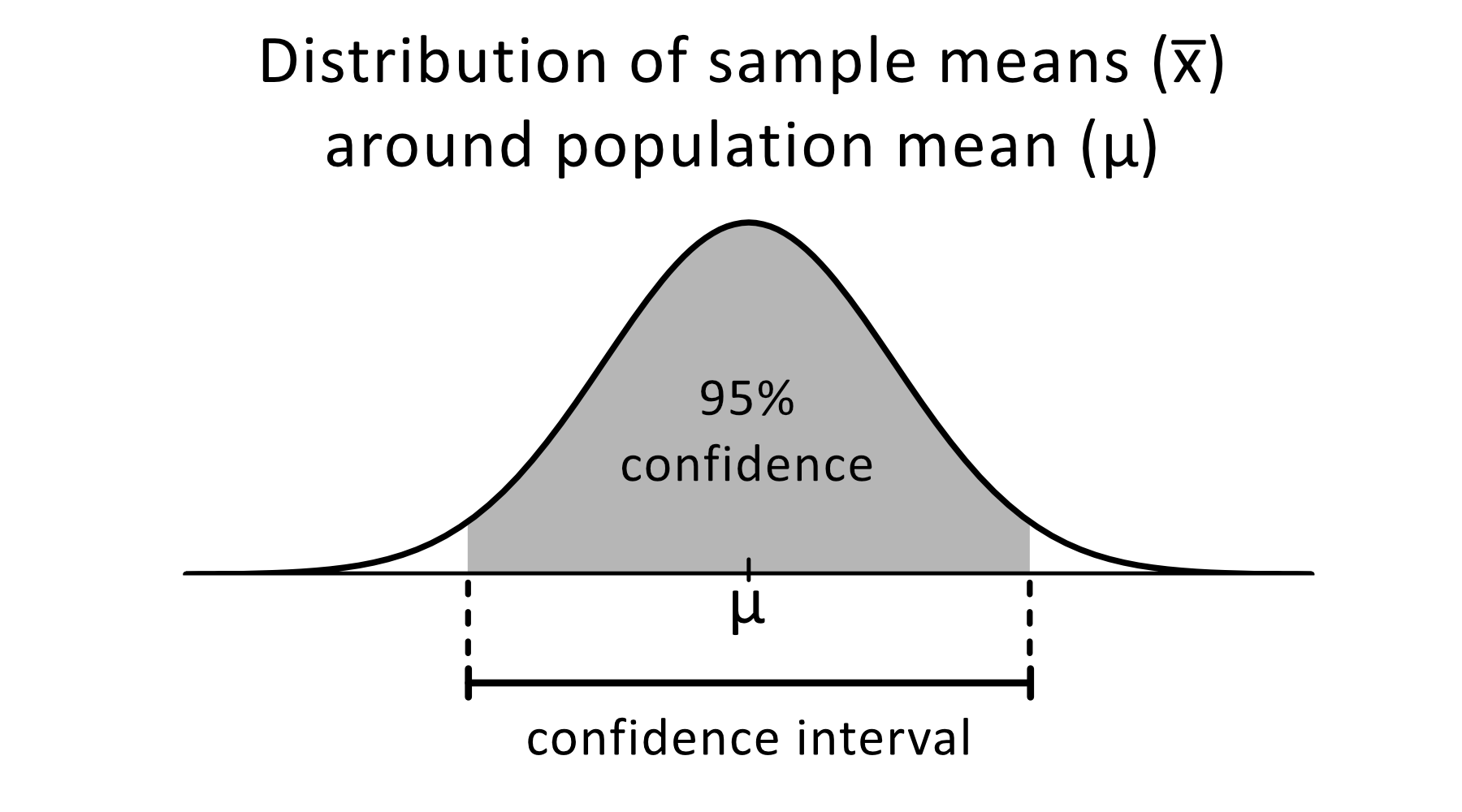
Where is the sample mean s is the sample standard deviation and k 2 is a factor for a two-sided tolerance interval defining the number of sample standard deviations required to cover the desired proportion of the population.Įxact values of k 2 are tabularized in ISO 16269-6. Two-sided Tolerance intervals are calculated as: The difference in location of the mean due to this uncertainty is defined by the confidence interval. The dotted line distributions result from the uncertainty of knowing the true location of the population mean. The solid line represents the actual population distribution.
The confidence level indicates the likelihood that the interval covers the desired proportion of the population.įigure 2: graphical depiction of a tolerance interval. This uncertainty is represented by the confidence level associated with the interval. This is because the tolerance interval must take into account the uncertainty of knowing the true location of the mean of the population distribution.

Notice in figure 2 that the interval range extends beyond the tail areas of the actual population distribution (solid line). A tolerance interval can be used for this purpose.įigure 2 depicts a tolerance interval graphically. Therefore, In order to maintain a reasonably accurate estimate of the capability of a process for smaller sample sizes, we need to adjust the number of multiple sample standard deviations used to define the region covering the desired proportion of the population distribution with a given confidence. As the sample size decreases, there is greater uncertainty in knowing the true location of the mean and the true magnitude of the population variance therefore, the estimate of the range of values encompassing a given percentage of the population must necessarily increase to compensate. But this percentage only holds true for larger sample sizes that is, greater than 50. This is because capability is usually calculated to cover a fixed multiple of sample standard deviations (usually ☓ representing 99.73% of the data population). In traditional statistical process control, a significant number of data points are required in order to get a reasonably accurate estimate of process capability.
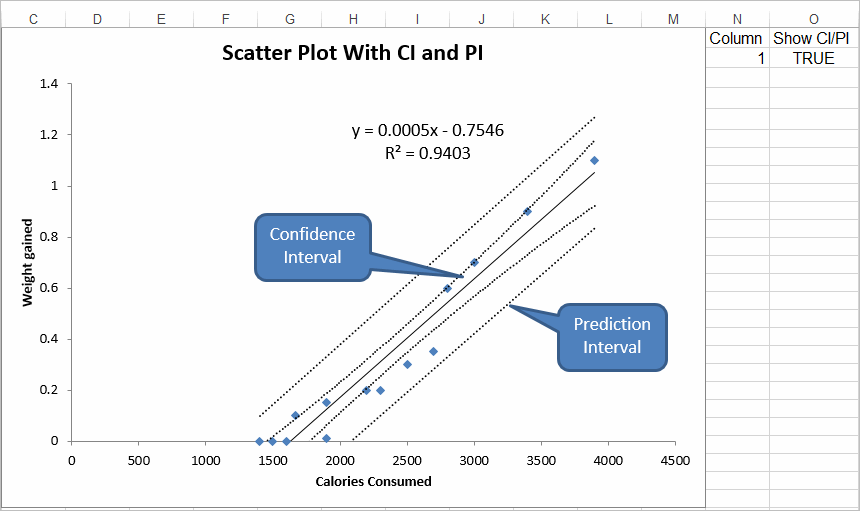
Instead, a small sample of a total population is inspected or tested and the data used to gauge how well the entire production batch conforms to specifications. Notice also that the capability of a process is determined not just by the location of the sample mean, but the tail areas of the distribution as well.īecause of physical, time or cost constraints, it is often impractical to inspect or test an entire production batch. The distribution on the right, on the other hand, exhibits poor capability the tail areas of this distribution fall outside of specification range. Looking at Figure 1, we can see that the distribution on the left exhibits good capability the tail areas of this distribution are well within the specification range. The capabilities of two different processes are depicted in Figure 1.įigure 1: Population distributions from two different processes compared against a specification range. Larger ratios indicate a more capable process while smaller ratios indicate a less capable process. This type of interval is called a tolerance interval and is closely related to measures of process capability.Ĭapability is usually expressed as the ratio of the specification range or tolerance for the measured characteristic to the observed variation associated with the characteristic. In this, the third and final statistical interval to be discussed, we will look at an interval to cover a specified proportion of a population distribution with a given confidence. In Part II we saw how a prediction interval can be calculated to define a region within which a single future observation or a multiple number of single future values is likely to be located with a given confidence.
Tolerance interval plot series#
We saw in Part I of this series how a confidence interval can be calculated to define a range within which the true value of a statistical parameter such as a mean or standard deviation is likely to be located with a given confidence.


 0 kommentar(er)
0 kommentar(er)
